
This lesson will cover the difference quotient, and how to use it to find derivatives.
This lesson includes a video lecture, a short self-grading test, a practice worksheet, and a solution sheet in the resources section. It is important to do the practice worksheet, as the self-grading test will not thoroughly check your mastery of the lesson.
The difference quotient is the basis for finding all derivatives, though most of this section of the class will be devoted to learning short cuts for different types of functions. In this lecture we discuss what a derivative is, and why the difference quotient works. However, I would not worry too much about this for now! You will not really need to understand what a derivative is, or what it means, or why it matters, until you get to Applications of Derivatives. For now, focus on mastering finding derivatives. This video will include several examples of using the difference quotient to find derivatives of given functions.
This video will go over the practice worksheet, demonstrating step-by-step solutions to problems from the worksheet.

This lesson introduces the short cut for finding the derivatives of basic polynomials, laying the ground work for many of the methods we will be covering in this course.
This lesson includes a video lecture, a short self-grading test, a practice worksheet, and a solution sheet in the resources section. It is important to do the practice worksheet, as the self-grading test will not thoroughly check your mastery of the lesson.
As discused in the last lesson, most of this class will actually be learning short-cut methods to find derivatives. This method works for polynomial functions, and is very quick and easy! Make sure you're comfortable with it before moving forward, as you will be using it a lot througout Calculus!
This video will go over the practice worksheet, demonstrating step-by-step solutions to problems from the worksheet.

This cover some less obvious applications of the methods learned in "Basic Derivatives".
This lesson includes a video lecture, a short self-grading test, a practice worksheet, and a solution sheet in the resources section. It is important to do the practice worksheet, as the self-grading test will not thoroughly check your mastery of the lesson.
This is essentially the same method as the last lesson, but includes negative and fraction exponents.
This video will go over the practice worksheet, demonstrating step-by-step solutions to problems from the worksheet.

This lesson covers Chain Rule, a very important method to master for taking derivatives.
This lesson includes a video lecture, a short self-grading test, a practice worksheet, and a solution sheet in the resources section. It is important to do the practice worksheet, as the self-grading test will not thoroughly check your mastery of the lesson.
The Chain Rule will be used constantly throughout Calculus, and is where many students begin to struggle. If you are prone to writing your work in an all-over-the-page style, now is a good time to cultivate a neater, more formal system. Clearly write each step. You may be able to skip some steps, and that's fine, but everything you write should be clearly labeled, with an equal sign, not just floating there. Indicate what a string of numbers and variables equals, rather than just leaving it there - is it u, u', f(x), f(u), f'(x), f'(u), what? It's important to keep track. I cannot stress this enough. Many very bright students are able to get this far in math without developing a neat style for keeping track of their work, because they're able to track it all in their head, and this is where it starts to catch up with them! From here on, Calculus problems can get very messy, with many parts. It is very important to keep track of which parts are what, so you don't make small mistakes and ruin an entire problem. The problems in this lesson are relatively simple, compared to some we'll be getting to, so use this lesson to get into the habit of writing work neatly.
This video will go over the practice worksheet, demonstrating step-by-step solutions to problems from the worksheet.
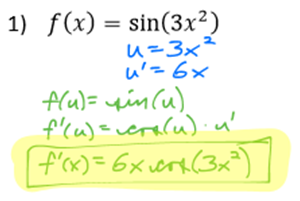
This lesson covers many derivative rules that you will need to know as you continue through Calculus.
You will need to use Chain Rule to solve these problems. Assume you will need Chain Rule for the rest of Calculus!
This lesson includes a video lecture, a short self-grading test, a practice worksheet, and a solution sheet in the resources section. It is important to do the practice worksheet, as the self-grading test will not thoroughly check your mastery of the lesson.
These are some common function types you will need to be able to take derivatives of throughout Calculus. The worksheet includes a reference box, and you should add these rules to your "cheat sheet", or memorize them, as you will need them throughout Calculus.
This video will go over the practice worksheet, demonstrating step-by-step solutions to problems from the worksheet.
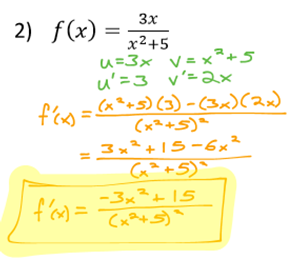
This lesson introduces the Product Rule and Quotient Rule, which are both very commonly used in Calculus.
You will need Chain Rule and the rules from "More Derivative Rules" for this lesson. Again, assume you will need these for the rest of Calculus!
This lesson includes a video lecture, a short self-grading test, a practice worksheet, and a solution sheet in the resources section. It is important to do the practice worksheet, as the self-grading test will not thoroughly check your mastery of the lesson.
The Product Rule and Quotient Rule are very common techniques for taking derivatives of functions that would otherwise be very difficult to work with. Note that as we continue through this class, each new lesson will require what you learned in the last one.
The lessons covered so far, from Basic Derivatives to this one, are what I would consider the basics of differentiation. Make sure you have mastered these skills!
This video will go over the practice worksheet, demonstrating step-by-step solutions to problems from the worksheet.
This test will check your understanding of everything in this section so far, lessons "The Difference Quotient" to "Product and Quotient Rules"
The solution sheet is in the Resources section.
If you are preparing for an AP exam or similar, your should take this test closed-book, closed-notes.
Otherwise, you should have a single "cheat sheet" with rules or formulas you might need. I recommend anything that's been in a Reference box as the top of a practice worksheet be either memorized or included on your "cheat sheet".
You may use a graphing calculator or regular calculator on this test.
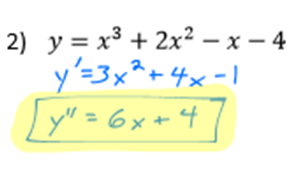
This introduces the concept of higher order derivatives.
This lesson includes a video lecture, a short self-grading test, a practice worksheet, and a solution sheet in the resources section. It is important to do the practice worksheet, as the self-grading test will not thoroughly check your mastery of the lesson.
Second and third derivatives are pretty much exactly what they sound like, there are really no new skills in this lesson! Consider this a good opportunity to practice the skills you've already learned, while mastering a new concept.
This video will go over the practice worksheet, demonstrating step-by-step solutions to problems from the worksheet.
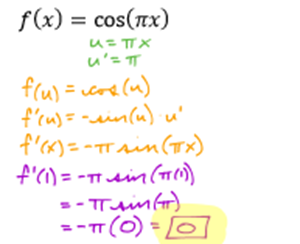
This covers how to find derivatives and second derivatives at exact x-values.
This lesson includes a video lecture, a short self-grading test, a practice worksheet, and a solution sheet in the resources section. It is important to do the practice worksheet, as the self-grading test will not thoroughly check your mastery of the lesson.
This is another pretty easy lesson, and more good practice taking derivatives!
This video will go over the practice worksheet, demonstrating step-by-step solutions to problems from the worksheet.
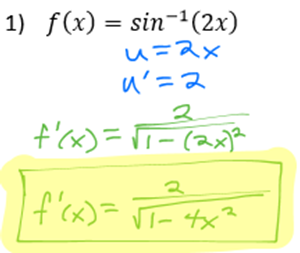
This introduces the rules for taking the derivatives of inverse trig functions.
This lesson includes a video lecture, a short self-grading test, a practice worksheet, and a solution sheet in the resources section. It is important to do the practice worksheet, as the self-grading test will not thoroughly check your mastery of the lesson.
The derivatives rules for inverse trig functions can be intimidating for some students, as they have some fairly large, messy fractions and radicals, but don't let that overwhelm you! These rules are large, but not really any more difficult than any of the rules you learned in "More Derivative Rules". As additional good news, you don't really use them much! I would include these rules on your "cheat sheet", but if you are not preparing for an AP or similar exam, I wouldn't bother memorizing them, and some classes may even skip them entirely. Nevertheless, they are good to be familar with.
This video will go over the practice worksheet, demonstrating step-by-step solutions to problems from the worksheet.
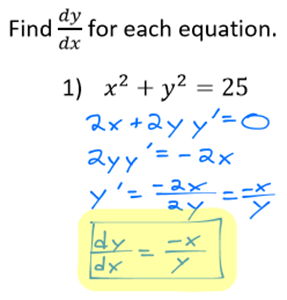
This introduces the implicit differentiation method.
This lesson includes a video lecture, a short self-grading test, a practice worksheet, and a solution sheet in the resources section. It is important to do the practice worksheet, as the self-grading test will not thoroughly check your mastery of the lesson.
Implicit Differentiation is less commonly used than most of the methods we've covered in this class, but important to master for later Calculus. You will definitely be using it in Applications of Derivatives, especially word problems involving optimization. If you are taking any kind of Physics or Engineering classes, or plan to be in the future, this is a technique that will come in handy there as well.
This can be one of the more difficult concepts for some students, and is pretty Algebra-heavy. Take your time and go through the lesson carefully.
This video will go over the practice worksheet, demonstrating step-by-step solutions to problems from the worksheet.
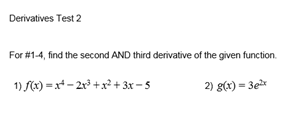
This will test your understanding of the lessons from "Second and Third Derivatives" to "Implicit Differentiation".
The solution sheet is in the Resources section.
If you are preparing for an AP exam or similar, you should take this test closed-book, closed-notes.
Otherwise, you should have a single "cheat sheet" with any rules or formulas you might need. I recommend including anything from a Reference box on the top of a practice worksheet.
You may use a graphing calculator on this test.
